ПРАКТИКУМ ПО MATLAB


 
  Анотація   Практикум

 
 
АНОТАЦІЯ

Система MATLAB позиціонується як математична лабораторія для моделювання та аналізу різноманітних систем. Це дуже потужна система, але дуже важка для її професійного опанування. Та треба зауважити, що "не боги обпалюють горщики". Необхідно також зауважити, що кожна з моделюючих підсистем в складі MATLAB, скоріше за все, потребує окремого посібника або навіть підручника. Тому на цій сторінці ми приділимо увагу лише необхідному мінімуму, що дозволить легше опанувати роботу з цією системою. В складі такого мінімуму важливо розглянути роботу з масивами, а також опанувати вбудовану в MATLAB мову програмування.

Для того, щоб було легше опановувати матеріал, в посібнику наведені приклади, що вже розглядалися на сторінці "Чисельні методи". Та основна увага приділяється поступовому опануванню мови MATLAB, де поряд з теоретичним матеріалом наведено ілюстративні приклади. Тексти таких прикладів можна легко копіювати в буфер комп'ютера та потім вставляти в консоль MATLAB для виконання.

 
  

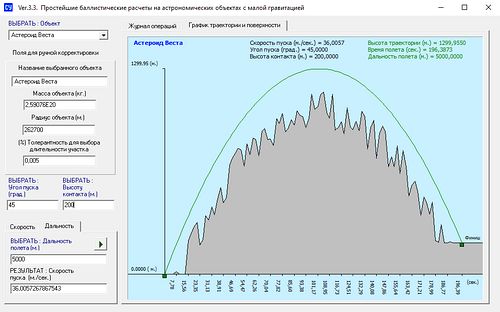
Окремо наведені приклади практичних задач. Особливо необхідно звернути увагу на задачу “ЛОГИСТИЧЕСКАЯ ЗАДАЧА НА ПОВЕРХНОСТИ АСТЕРОИДОВ”. Ця задача ілюструє в найпростішому вигляді застосування методу кінцевих елементів, який застосовується до аналізу складних систем, що неможливо змоделювати одним алгебраїчнім або диференційнім рівнянням.

Також окремої уваги заслуговує задача апроксимації табличних функцій в довільному базисі. Така апроксимація дуже корисна, коли відомо, що математична модель системи дуже близька до лінійної комбінації декількох аналітичних функцій.

Спираючись на приклади, що наведені у посібнику та до посібника, ви зможете самостійно створювати необхідні вам інструменти аналізу та розрахунків в складі ваших засобів автоматизації роботи.

 
 


 
 
ЛАБОРАТОРНЫЙ ПРАКТИКУМ ПО MATLAB
 
ЗМІСТ
  • ВСТУП
  • АННОТАЦІЯ ДО ТЕМАТИЧНОЇ СТРУКТУРИ ПРАКТИКУМУ
  • 1. ПОЧАТКОВИЙ ЗНАЙОМСТВО З MATLAB. (ЛАБ. РОБОТА 1)
  • 1.1. ФОРМА БЭКУСА — НАУРА.
  • 1.1.1. Терміни БНФ
  • 1.1.2. Спеціальний нетермінал "Пусто"
  • 1.1.3. Оператор визначення
  • 1.1.4. Основне правило БНФ
  • 1.1.5. Оператор выбора
  • 1.1.6. Рекурсивне правило БНФ
  • 1.1.7. Спеціальні розширення стандарту БНФ
  • 1.2. ЗНАЙОМСТВО З ПОДАННЯМ ДАНИХ У СИСТЕМІ MATLAB
  • 1.2.1. Типи арифметичних чисел у MATLAB
  • 1.2.2. Знайомство з коментарями, константами та змінними, з простими арифметичними операціями
  • 1.2.3. Вираз. Простий арифметичний вираз
  • 1.2.4. Синтаксис простого арифметичного виразу
  • 1.2.5. Приклади арифметичних виразів
  • 1.3. САМОСТІЙНА РОБОТА
  • 2. MATLAB – ЦЕ МАТРИЦІ (ЛАБ. РОБОТА 2)
  • 2.1. СТВОРЕННЯ МАТРИЦЬ І МАНІПУЛЯЦІЯ ЕЛЕМЕНТАМИ МАТРИЦЬ
  • 2.1.1. Визначення одновимірних матриць (векторів)
  • 2.1.2. Приклади створення одновимірних матриць (векторів)
  • 2.1.3. Визначення прямокутних матриць (2D-матриць)
  • 2.1.4. Приклади створення прямокутних матриць (2D-матриць)
  • 2.1.5. Правила доступу до структур усередині матриць
  • 2.1.6. Приклади доступу до структур усередині матриць
  • 2.1.7. Матриці MATLAB це динамічні структури
  • 2.1.8. Приклади маніпуляції рядками та стовпцями чи субматрицями у 2D-матрицях
  • 2.1.9. Приклад динамічного зниження розмірів та розмірності 2D-матриці
  • 2.2. МАТРИЦІ З РОЗМІРНІСТЮ БІЛЬШ НІЖ 2D
  • 2.2.1. Приклад створення матриць 3D
  • 2.2.2. Приклад маніпуляції значеннями та розмірністю матриць 3D
  • 2.2.3. Декілька слів про матриці розмірністю 4D і вище
  • 2.2.4. Сервісні функції MATLAB для роботи з матрицями
  • 2.3. . ОПЕРАЦІЇ З МАТРИЦЯМИ В MATLAB
  • 2.3.1. Операція транспонування
  • 2.3.2. Поелементні операції для арифметичних матриць
  • 2.3.3. Одномісні поелементні операції для арифметичних матриць будь-якої розмірності
  • 2.3.4. Двомісні поелементні операції для арифметичних nD–матриць та простого арифметичного операнда (скаляра)
  • 2.3.5. Двомісні поелементні операції для арифметичних nD–матриць однакової розмірності та розміру
  • 2.4. САМОСТІЙНА РОБОТА
  • 3. ПОБУДОВА ГРАФІКІВ (ЛАБ. РОБОТА 3)
  • 3.1. PLOT - ПОБУДОВА ГРАФІКІВ, ЗАДАНИХ МАТРИЦЯМИ
  • 3.1.1. функція PLOT. Синтаксис
  • 3.1.2. функція PLOT. Приклади
  • 3.2. FPLOT - ПОБУДОВА ГРАФІКІВ, ЗАДАНИХ АНАЛІТИЧНО
  • 3.2.1. Функція FPLOT. Синтаксис
  • 3.2.2. . Функція FPLOT. Приклади
  • 3.3. ФУНКЦІЯ AXIS
  • 3.3.1. функція AXIS. Синтаксис
  • 3.3.2. функція AXIS. Приклади
  • 3.4. EZPLOT. ПРОСТОЙ В ВИКОРИСТАННІ ПЛОТТЕР
  • 3.4.1. Функція EZplot. Синтаксис
  • 3.4.2. Функція EZplot. Опис
  • 3.4.3. Функция EZplot. Примеры
  • 3.5. EZPOLAR. ПРОСТИЙ В ВИКОРИСТАННІ ПОЛЯРНИЙ КООРДИНАТНИЙ ПЛОТТЕР
  • 3.5.1. функція EZPOLAR. Синтаксис
  • 3.5.2. функція EZPOLAR. Опис
  • 3.5.3. функція EZPOLAR. Приклади
  • 3.6. САМОСТІЙНА РОБОТА
  • 4. УМОВНІ ВИРАЗИ, ОПЕРАТОРИ РОЗГАЛУЖЕННЯ, ЦИКЛИ (ЛАБ. РОБОТА 4)
  • 4.1. УМОВНІ ВИРАЗИ (CONDITIONAL EXPRESSION)
  • 4.1.1. Оператори відносин (Relational operations)
  • 4.1.2. Приклади операторів відносин
  • 4.1.3. Обчислення відносин алгоритмічним шляхом
  • 4.1.4. Логічні оператори та операції (Logical operations)
  • 4.1.5. Деякі закони для логічних операцій
  • 4.2. УМОВИ ОПЕРАТОРИ (ІНСТРУКЦІЇ)
  • 4.2.1. Простий умовний оператор if
  • 4.2.2. Селектор з різних умов if..elseif
  • 4.2.3. Селектор за різними значеннями
  • 4.3. ЦИКЛИ
  • 4.3.1. Цикл FOR
  • 4.3.2. Цикл FOR. Приклади
  • 4.3.3. Цикл WHILE
  • 4.3.4. Цикл WHILE. Приклади
  • 4.4. САМОСТІЙНА РОБОТА
  • 5. СКРИПТИ І ФУНКЦІЇ (ЛАБ. РОБОТА 5)
  • 5.1. ВСТУП
  • 5.2. СКРИПТИ
  • 5.2.1. Правило оформлення help для скриптів
  • 5.3. ФУНКЦІЇ
  • 5.3.1. Синтаксис функцій
  • 5.3.2. Глобальні та локальні змінні
  • 5.3.3. Виклик функцій
  • 5.3.4. Основні правила роботи з функціями
  • 5.3.5. Функції. Приклади
  • 5.4. САМОСТІЙНА РОБОТА
  • 6. РІШЕННЯ СИСТЕМ ЛІНІЙНИХ РІВНЯНЬ. (ЛАБ. РОБОТА 6)
  • 6.1. РІШЕННЯ СИСТЕМИ ЛІНІЙНИХ РІВНЯНЬ МЕТОДОМ КРАМЕРА
  • 6.1.1. Основна ідея методу
  • 6.2. ТЕОРЕМА КРОНЕКЕРА-КАПЕЛЛІ
  • 6.3. РІШЕННЯ СИСТЕМИ ЛІНІЙНИХ РІВНЯНЬ МЕТОДОМ ГАУСА
  • 6.3.1. Основна ідея методу
  • 6.3.2. Метод виключення довільної змінної із зазначеного рівняння у системі лінійних рівнянь
  • 6.3.3. Метод побудови трикутної матриці шляхом послідовного виключення змінних
  • 6.4. РІШЕННЯ СИСТЕМ ЛІНІЙНИХ РІВНЯНЬ. ПРИКЛАДИ
  • 6.4.1. Реалізація методу Крамера
  • 6.4.2. Вирішення систем лінійних рівнянь засобами MATLAB. Приклади
  • 6.4.3. Реалізація методу Гауса. Приклади
  • 6.4.4. Порівняльні тести методів розв'язання SLE
  • 6.5. САМОСТІЙНА РОБОТА
  • 7. АППРОКСИМАЦІЯ ТАБЛИЧНО-ЗАДАНОЇ ФУНКЦІЇ. (ЛАБ. РОБОТА 7)
  • 7.1. ПОСТАНОВКА ЗАДАЧІ
  • 7.2. ЗАДАЧА АППРОКСИМАЦІЇ У ДИСКРЕТНІЙ ФОРМІ
  • 7.2.1. Побудова умов для вирішення задачі апроксимації у дискретній формі
  • 7.2.2. Розв'язання задачі апроксимації у дискретній формі
  • 7.3. РЕАЛІЗАЦІЇ МЕТОДІВ НАЙМЕНШИХ КВАДРАТІВ
  • 7.3.1. Метод найменших квадратів для базисних функцій x^n
  • 7.3.2. Метод найменших квадратів для довільних базисних функцій
  • 7.4. САМОСТІЙНА РОБОТА.
  • СПИСОК ЛІТЕРАТУРИ
  • ДОДАТКИ
  • ДОДАТОК А. ЗАДАЧА СТИКУВАННЯ ЧОВНИКА ТА СТАНЦІЇ
  • Постановка задачі
  • Математичний аналіз задачі
  • Вихідні дані та завдання
  • Зміст роботи
  • ДОДАТОК Б. 3D-ГРАФІКИ В MATLAB
  • Постановка задачі
  • 1. Функція meshgrid
  • 2. Функція mesh, meshc, meshz
  • 3. Функція colormap
  • 4. Функція shading
  • 5. Функція view
  • 6. Функція surfl
  • Зміст роботи
  • ДОДАТОК В. ЛОГІСТИЧНЕ ЗАДАЧА НА ПОВЕРХНІ АСТЕРОЇДІВ
  • Вступ. Оцінка перспективності та актуальності задачі
  • Постановка задачі та зміст роботи
  • Аналіз задачі про рух тіла з постійним прискоренням
  • Аналіз завдання про вертикальний рух тіла у гравітаційному полі
  • Варіант рішення №1
  • Варіант рішення №2
  • Розв'язання задачі про вертикальний рух тіла у гравітаційному полі в середовищі MATLAB
  • Задача про рух тіла у гравітаційному полі, кинутого під кутом до горизонту
  • Рух тіла кинутого під кутом до горизонту за постійного прискорення вільного падіння
  • Рух тіла кинутого під кутом до горизонту із прискоренням вільного падіння, що залежить від висоти над поверхнею
  • Остаточне вирішення задачі у середовищі MATLAB
 
    
ПРИКЛАДИ
 
Скорочений лабораторний практикум (MATLAB):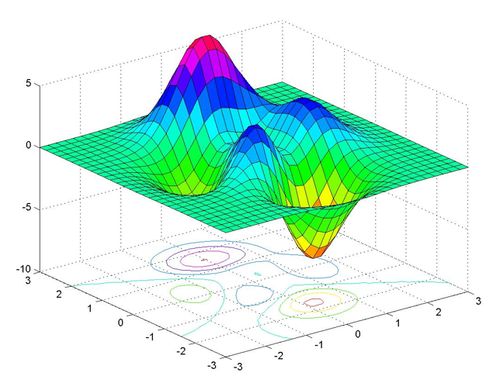  
 

Лаб3. Побудова 2D та 3D графіків

 
TXT-тексти з варіантами програмам загального призначення (MATLAB):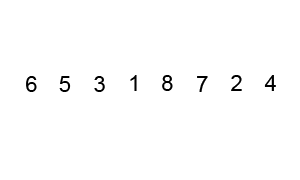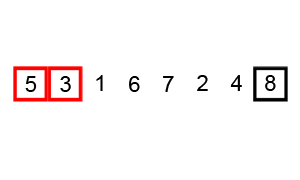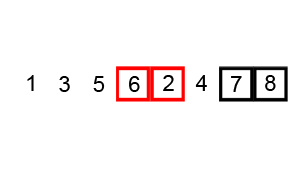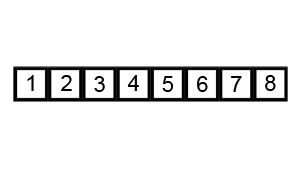  
 

Найпростіше бульбашкове сортування

 
Апроксімація таблічно заданих функцій (MATLAB):  
 
 
Балістика на астероїдах  
 
 
 
Калкулятор  
 

   
  До меню сторінки