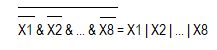Для початку дамо посилання на офіційну та довідкову документацію необхідну для дослідження та проектування цифрової сземотеніки.

Також, для зручного знайомства з цифровою електронікою, наведемо декілька важливих документів:

1. Лехин С.И. Схемотехника ЭВЬ.-СПб.:БХВ-Санкт-Петербург, 2010.-672 с.:ил. ISBN 5-9775-0353-2
   Цифровая схемотехника (.djvu)


2. Угрюмов Е.П. Цифровая схемотехника.-СПб.:БХВ-Санкт-Петербург, 2000.-528 с.:ил. ISBN 5-8206-0100-9
   Цифровая схемотехника (.djvu)


3. Портал електроніки з англомовної вікіпедії.
   Portal:Electronics


4. Каталог 01 URL-посилань з цифрової схемотехніки з англомовної вікіпедії.
   Цифрові схеми (.pdf)
   Category:Digital_circuits


5. Каталог 02 URL-посилань на інтегральні схеми з англомовної вікіпедії.
   Інтегральні схеми серії 7400 (.pdf)
   7400-series_integrated_circuits


6. Каталог 03 URL-посилань на інтегральні схеми з англомовної вікіпедії.
   Каталог посилань на інтегральні схеми серії 4000 (.pdf)
   4000-series_integrated_circuits

На сьогодні вже відома значна кількість систем моделювання електроніки. Але історично так склалося, що коли на початку 2000 року виникла для навчального процесу потреба в моделюванні електроних та електротехнічниних схем, відносно доступною виявилася система WORKBENCH. В подальши часи фірма National Instruments підтримала розвиток цього напрямку серією систем Multisim.

1. National Instruments Corporation, Multisim User Guide, переклад офіційної документації. — 491 с. : ил.
   Переклад User Guide (.pdf)


2. В квітні 2015 року компанія National Instruments анонсувала виход чотирнадцятої версії програмного середовища проектування електроних пристроїв Multisim & Ultiboard.
   Нові можливості Multisim_14 (.pdf)


3. Скорочена інструкція по застосуванню системи моделювання електроних пристроїв Multisim.
   Скорочена інструкція (.pdf)


4. Проектування та аналіз електричних схем в програмному середовищі Multisim. Методичні вказівки до самостійної роботи студентів.
   Методичні вказівки (.pdf)

Всі наведені на сторінці моделі представлені в Multisim версії 11 (в окремих випадках також в версії 8). Моделі спроектовані в Multisim верии 11 без проблем імпортуються в Multisim версії 14.

Заватажити архів моделей (*.7z). Архів включає 42 документовані моделі (.ms11, .pdf)

ЕЛЕМЕНТИ:

Логічні операції. Знайомство з цифровою електронікою завжди починається з таблиць істинності які відображують результати виконання простих логічних операцій NOT, OR та AND. Також для простих логічних операцій визначено декілька законів (перетворень логічних виразів) Закони логіки (.pdf). Опанування цих законів значно полегшуе розуміння роботи цифрових схем.

Наприклад, закон де Моргана, який встановлює зв'язок між операціями NOT, OR та AND, дозволяє зрозуміти чому лише єдина операція OR-NOT (Стрелка Пирса) або AND-NOT (Штрих Шеффера) дозволяють реалізувати операції NOT, OR та AND, а далі і всю логічну алгебру. Як цікавий схемотехнічний приклад можна навести наступе: операція AND-NOT (.jpg) та після подстановки інверсних аргументів (Q1,Q4) операція OR (.jpg) . Якщо вам зрозуміла робота цих схем, то можна сміливо рухатися далі.

Комбінаційні схеми. Комбінаційні схеми можна визначити як схемотехнічна реалізація простих або складніх логічних виразів, що включають в себе лише операції NOT, OR, AND та їх комбінації . Зазвичай до комбінаційних схем відносять різноманітні шифратори та дешифраторі кодів, а також реалізацію логічних або арифметичних функцій.

Наприклад: шифратор семисегментного коду операціями OR на діодах (.jpg). В такому шифраторі кожен сегмент індикатору вмикається операцієй OR, виконаної на діодах, а саму операцію можна реалізувати на швидких діодах, що значно розширює ії застосування.

Другий приклад стосується реалізації арифметичної функції: арифметичний суматор одного біту (.jpg). По першому варіанту реалізація суматора орієнтована на сприняття логіки та ії легке усвідомлення, а от у другому варіанті реалізація оптимизована для створення мікросхем і зовсім не прозора. Мабуть з цієї причини більшість розроблених комбінаційних схем розробники залишають не оптимизованими, що полегшує їх подальший супровід.

ФКІ та ГЕНЕРАТОРИ:

Затримки сігналів. Наступним важливим кроком є усвідомлення того, що електричні зв'язки між схемотехнічними реалізаціями логічніх єлментів завжди включають ємкостний або індуктивий характер. Тобто, логічні сигнали, що поступають на входи таких логічних єлементів можуть мати похілі фронти та різноманітні затримки. Крім того, по різним схемотехнічним ланцюжкам, попередні логічні єлементи також здатні створювати (завдяки своєї інерційності) відчутні затримки. Тому завжди необхідно враховувати наступне:

• Якщо на входах логічного елементу змінюється лише один сигнал, то зартимка на виході буде залежити лише від рівня сигналу (з похилим фронтом) що сприймається логічним елементом як логічна одиниця або нуль та затримкою в самому логічному елементі;
• Якщо на входах логічного елементу одночасно змінюється декілька сигналів, необхідно розглядати всі проміжні інтервали часу такої зміни, бо на тахих інтервалах можуть короткочасно виникати зовсім неочікувані комбінації логічних сигналів. Зрозуміло, що логічний єлемент може встигати опрацьовувати такі комбінаціі та формувати на своєму виході серію короткочасних та зовсім неочікуваних сигналів. Таке явище отримало назву " гонка сигналів ".

операція OR-NOT (.jpg)

ФКІ. Якщо кожна " медаль має зворотний бік ", то гонка сигналів також може слугувати для реалізації користних схем. До числа таких сжем можна віднести формувачі коротіх імпульсі по обраному фронту вхідного сигнала (ФКІ) та генератори імпульсів на затримках. Як приклад ФКІ наведемо
схему ФКІ, діаграми роботи та теоретичні викладки (.pdf).

Генератори. В цьому підрозділі розглянуто моделі генераторов прямокутних імпульсів стабільність частоти яких не потребує високих вимог. Нажаль моделі стабільних генераторів з кварцевими резонаторами змоделювати в MultiSim не вдається, якщо в схемах застосовується лише логічні елементи. Тому класичні кварцові генератори на логічних елементах винесені за дужки.

Самий простий генератор можна реалізувати на двох RC-затримках (С2 >= С1) та інверторами з тригерами Шмідта, що забеспечує чітке реагування на похилий фронт на виході RC-ланцюжків. Генератор на затримках (.jpg) )

Також простий генератор можна реалізувати на двох ФКІ. Така реалізація дозволяє незалежно обирати довжину імпульса та паузи. Якщо необхідно встановити довгу паузу, то ії краще формувти за допомогою таймеру серіі 555. Генератор на ФКІ (.jpg) )

Якщо вам необхідно створити максимально стабільний генератор без застосування кварцеого резонатору, то добрим рішенням буде використання таймеру серіі 555. Це обумовлено тим, що рівень напруг для кордонів логічної одиниці або нуля визначається в таймері точними аналоговими компораторами. Таким чином, стабільнісь такого генератора буде залежна лише від стабільності пасивних елементів (резисторів та конденсаторів)
Генератор на таймері серіі 555 (.jpg) )

ТРИГЕРИ:
Тригер можна розглядати як елемент пам'яті разрадністю один біт. Любий тригер має декілька входів установки з допомогою яких він перемикається по виходам з нуля в единицю або навпаки. Крім того, на входах обов'язково визначається комбинація сигналів що відповідае стану збереження його поточного стану. В комбінації збереження на виході тригера зберігається або нуль або одиниця, тобто при одній комбинації на вході маємо дві комбінації на виході. З цієї причини тригер не можливо формалізувати лише комбінаційною логікою і для його формалізації визначаються різні мови кінцевих автоматів.

Тригер має два входи (set-установка вихода Q в одиницю та reset-установка вихода Q в в нуль. Визначимо вхідні комбінації для такого тригера:

• Комбінація збереження стану - це одиниці на обох входах (set=1, reset=1)
• Комбінація установки вихода Q в стан одиниці (set=0, reset=1)
• Комбінація установки вихода Q в стан нуля (set=1, reset=0)
• Заборонена комбінація входних сигналів (set=0, reset=0)

Комбінації: --> (set=0, reset=1) --> (set=1, reset=1)

Розглянемо установку вихода тригера Q в одиницю, тобто (set=0, reset=1). Сигнал (set=0) призведе до того, що на виході елементу Е1 буде встановлена одиниця незалежно від того який сигнал X буде на другому вході елемента Е1. Дійсно, (вихід Е1) = not (0 and X)=1.
Далі, (вихід Е2) = not [ (вихід Е1=1) and (reset=1) ]=0, тобто (вихід Е2) це інверсний вихід для (вихід Е1).
Але важливо інше, якщо сигнал set повернути до одиниці (set=1, reset=1), то значення сигналів на входах елемента Е1 лише дзеркально змінятся, а сигнали на виходах Е1 та Е2 залишаться без зміни, тобто ми не лише виконали установку тригера, а ще і перешли до стану збереження.

Не важко здогадатися, якщо схема тригера дзеркальна відносно елементів Е1 та Е2, то установка тригера, сигналом (set=1, reset=0) має вже розглянуту логіку, а комбінація (set=1, reset=0) це дійсно утановка вихода тригера Q в нуль.

Проблема комбінації: (set=0, reset=0) --> (set=1, reset=1)

Але особливо необхідно розглянкти реакцію тригера на перехід від забороненої вхідної комбінації (set=0, reset=0) до комбінації збереження (set=1, reset=1). Типово, такі переходи виникають коли вмикаєтся живлення приладу, або якщо попередня логіка, що формує сигнали на входах тригера, має різні затримки та здатна формувати короткочасні проміжні сигналі (детально ми розглядали це в розділі ЛОГІЧНІ ЕЛЕМЕНТИ).

Проблема переходу від (set=0, reset=0) до (set=1, reset=1) полягає в тому, що не можна визначити в якому стані буде завершено такий перехід, тобто невідомо одиниця чи нуль залишаться на Q-виході тригера. Дійсно, після комбінації (set=0, reset=0) на виходах Е1 та Е2 примусово утворюються одиниці, а при включенні комбінації (set=1, reset=1) оба елемента Е1 та Е2 мають перейти в стан нуля, що дзеркально змінюе ситуацію. Тому невідомо, який з елементів встигне швидше виконати переключення та відповідно виграти гонку переключень. В окремих (дуже рідких випадках) внутрішні затримки настільки ідентичні що починається безперервна генерація. В папці (1 Триггеры и Счетчики\1 Триггеры\1 RS-Триггер\2 Проблемы) можна знайти відповідні моделі.

Вирішення проблеми переходу (set=0, reset=0) --> (set=1, reset=1)

У випадку вмикання живлення, та і в інших багатьох випадках, коли необхідна початкова утановка схеми, в тригери влючаеться додатковий вхід з назвою СКИНУТИ, скорочено CLN або CLR (clean або clear). Таку модифікацію тригера у найвпрстішому вигляді можна зобразити наступним чином: логіка входу СКИНУТИ (.jpg) . Для формування сигналу CLN при вмиканні живлення застосовується повільний заряд конденсатора від джерела живлення.

У випадку різноманітних затримок вхідних сигналів, единим гарантованим рішенням є дочекатися коли всі затримки закінчаться і лише потім дозволити сигнали установки тригера. Таке рішення мпє назву СИНХРОНІЗАЦІЯ, а відповідні тригери називаються синхроними. Синхроні тригера, в свою чергу, поділяют на однотактні та двотактні. Однотактні тригера змінюють свій стан відразу, коли з'являється сигнал сінхронізації, а двотактні змінюють свій стан коли сигнал синхронізації завершується, тобто в кінці імпульса синхронізації.

Розглянемо найпростіше схемотехнічне рішення однотактного синхроного RS-тригера: однотактний синхронний RS-тригер (.jpg) . Традиційно сигнал синхронізаціїї має назву СІНХРО або CLK(clok). В наведеній схемі зміна стану тригера відбувається доки тримається сигнал синхронізації (установка). Недоліком однотактного синхронного тригера є необхідність гарантовано дочекатися кінця переходних процесів в вузлах на вході тригера, тобто, потребує додаткових схемотехнічних рішень.

Схема найпростішого двотактного синхроного RS-тригера наведена на малюнку; Двотактний синхроний RS-тригер (.jpg) . Такий тригер послідовно вкючає в себе два однотактних RS-тригера. Поки перший тригер відслідковує вхідні сигнали по сигналу CLK, другий тригер по інверсному CLK знаходиться в стані збереження, тобто ізолюе на свеєму виході перехідні процеси що відслідковуються першим тригером. При завершенні CLK малюнок дзеркально змінюєтся, другий тригер копіюе в себе стан першого, а перший переходить в стан збереження, чим також виконує ізоляцію вхідних сигналів. Таке рішення дозволяє довжиною імпульса CLK визначати максимальний час для завершення всіх перехідних процесів на вході двотактного тригера.

Крім того, двотактний синхроний RS-тригер легко модифікуються в найпростіший: одноразрядний бінарний лічильник імпульсів (.jpg) , який традиційно має назву Т-тригер. Для цього необхідна лише одна або дві додаткових ліній з'вязку. В моделі (1 Триггеры и Счетчики\2 Счетчики\1 Логика\1 ПростейшийСчетчик) наведено полубайтовий лічильник імпульсяв, де одноразрядні бінарні лічильники реалізовані з двома додатковими лініями з'вязку.

Заключний коментар з приводу синхронізації

Якщо ми маємо декілька скінченних автоматів (спрощено, схем з тригерами та комбінаційною логікою на входах та виходах) що включені послідовно, то нам, скоріше за все, знадобится щось накшталт многофазного гекератора коротких імпульсів (такі генератори ми вже розгядали в розділі ФКІ та ГЕНЕРАТОРИ). Послідовно в часі тактові імпульси таких генераторів дають змогу дочикатися поки сигнали на входах тригерів набудуть завершеного вигляду для кожного автомату.

D-, JK- ТРИГЕРИ:

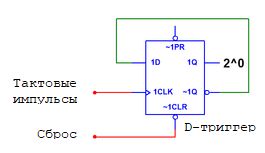
D-тригер є логічною модифікацією двотактного синхронного RS-тригера. Найпростішу логічну схему D-тригера ми вже фактично розгядали, коли входи двотактного синхронного RS-тригера об'єднали з допомогою інвертора в один вхід з назвою D, надавши йому сенсу вхідні данні (data).
D-тригер на базі двотактного RS-тригера (.jpg)

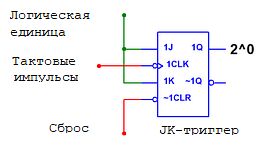
JK-тригер також можна розглядати, як логічну модифікацію двотактного синхронного RS-тригера. Типово тригер має три входи: тобто CLK, J (Jump) швидке вмикання та K (Kill) швидке вимикання. При (J=K=1) JK-тригер працює як двотактний Т-тригер. При (J=0, K=1) або (J=1, K=0) JK-тригер працює як двотактний RS-тригер, де вход J аналогічен S входу RS-тригера, а вход K аналогичен входу R. При (J=0, K=0) тригер не реагує на імпульси CLR та зберігає поточний стан, тобто JK-тригер не має заборонених вхідних комбінацій. Хоча JK-тригер позиціанується як універсальний, для реалізації на його бізі D-тригера необхідно додати зовнішній інвертор з входу J на вхід К.
JK-тригер на базі двотактного RS-тригера (.jpg)

Заключний коментар з приводу тригерів

На цій сторінці ми розглянули структуру та логіку найбільш вживаних в схемотехниці тригеров, при цьому (для логічної прозорості) винесли за дужки оптимізацію структри в прикладах. До речі, в архіві розглянуто значна кількість моделей відображаючих різноманітні модифікації тригеров. Додаткову інформацію можна отримати з огляду тригерів на вікопедії: Тригери (.pdf)

T-ТРИГЕРИ, ЛІЧИЛЬНИКИ ІМПУЛЬСІВ:

Базовим елементом лічильників можна важати T-тригери. На малюнку, що наведений нижче, показанно модифікації JK- та D-тригерів у T-тригер.

Особливостю T-тригера є зміна його стану з нуля в одиницю або навпаки на кожний тактовий імпульс, тобто період сигналу на виході T-тригера в два рази довший ніж реріод тактових імпульсів. Якщо створити ланцюжок з Т-тригерів такий, що вихід попереднього тригера (Q) приєднується к тактовому входу (CLK) наступного тригера, то на виходах тригерів ланцюжка кожний наступний тактовий імпульс буде послідовно формувати бінарних код. На малюнку, що наведений нижче, показана відповідна осцилограма для лічильника прямого рахунку (модифікація з JK-тригерами).

Тобто, осцилограма ілюструе роботу лічильника із зростаючим бінарним кодом полубайтової разрядності. Але, якщо застосувати в ланцюжку інверсні виходи Т-тригерів, то бінарний код буде змінюватися вже не у прямому, а в зворотньому напрямку. Перемикання між напрямком рахунку можна виконати дуже простими комбінаторними схемами і, в такому випадку, ми отримаємо універсальний (реверсійний) бінарний лічильник. Модеді таких найпростіших лічильників наведені в папці (1 Триггеры и Счетчики\2 Счетчики) в складі архіву. В професійних рішеннях ревесівних лічильників зазвичай також застосовується входи тригерів PR (Data Propagation delay/Затримка передачі даних), але ми разглядаємо лише логіку, тобто, у випадку реальних схем, зімість наведених прикладів, використовуються мікросхеми, де питання тонкої синхронізації вже врегульовані (наприклад, 74161N, 74F161AN, 74LS161N та інші).
Бнарний лічильник (.jpg) 74161_01.jpg

Важливою модифікацією бінарних лічильників можна разглядати лічильники з довільною основою рахунку, тобто, із основою рахунку 3, 5, 6, 7, 10, 12 та інше). В найпростішому випадку застосовуються відповідні дешифратори бінарного коду (тобто 3, 5, 6, 7, 10, 12 та інше), які відслідковують вихідний код бінарного лічильника та коли він досягає основи рахунку формують сигнал сбросу на асинхронний вхід лічильника. Тобто, замість переходу до коду основи рахунку лічильник повертається до коду нуля. В професійних рішеннях бажано, щоб тривалість імпульсу сбросу дорівнювала тривалісті тактового імпульсу. Нійбільш популярними мікросхемами лічильників з довільною основою рахунку є бінарно-десятичні лічильники (наприклад 74192N, 74F192N, 74LS192N та інші), які відображають кожну десятичну цифру у бінарному коді, наприклад:
Бнарно-десятичний лічильник (.jpg)

Інші приклади побудови розглянутих лічильників наведені в папці (Триггеры и Счетчики\2 Счетчики\2 Примеры) в складі архиву.

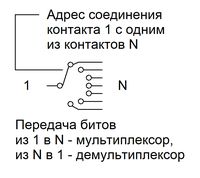
ЦИФРОВІ ПЕРЕМИКАЧІ:

ДЕМУЛЬТИПЛЕКСОРИ:
В якості приклада логіки побудови демультиплекора наведемо комбінаційну схему демультиплексора 1 в 16 (.jpg) . Побудова схеми включає один вхідний контакт (In1), на який подано загальний сигнал, 16 вихідних контактів (C0...CF), дешифратор бінарного коду в одиничний код адресу з'єднання, та 16 вмикачів на схемах AND. Якщо на вході (In1) зафіксувати логічну одиницю, то отримаємо звичайний перетворювач бінарного коду (А0...А3) в одиничний паралельний код.

Модель для тестування демультиплексора наведена в папці (ТЕМА 3 Переключатели Регистры\1 Переключатели\Логика\1 Демультиплексор)

МУЛЬТИПЛЕКСОРИ:
В якості приклада логіки побудови мультиплекора наведемо комбінаційну схему мультиплексора 16 в 1 (.jpg) . Побудова схеми включає 16 вхідних контактів (C0...CF) та один вихідний контакт (Out), дешифратор бінарного коду в одиничний код адресу з'єднання, та 16 вмикачів на схемах NOT AND. Виходи вмикачів за допомогою мікросхем 74S30N та за правилом де Моргана об'єднуються в комбінаційну OR з багатьма входами, що і зебеспечує перемикання каналів.

Моделі для тестування мультиплексорів наведені в папках (ТЕМА 3 Переключатели Регистры\1 Переключатели\Логика\2 Мультиплексор\Вариант1) та (ТЕМА 3 Переключатели Регистры\1 Переключатели\Логика\2 Мультиплексор\Вариант2)

РЕГІСТРИ:

ПАРАЛЕЛЬНІ РЕГІСТРИ:
Паралельні регістри призначені для одночасного зчитування та зберигання декілька бітів. Зазвичай паралельні регістри побудовані на синхроних D-тригерах з спільною синхронізацією (CLK лінія) та спільним CLR.
Модель паралельного регістру (.jpg)

Основне застосування паралельних регістрів це буферізація даних (типово байту або полубайту), а також фіксація стану бітів комбінаційних схем або скінченних автоматів з затримкою на завершення перехідних процесів.

Модель для тестування паралельного регістру наведена в папці (ТЕМА 3 Переключатели Регистры\2 Регистры\1 Параллельные\1 Логика)

РЕГІСТРИ ЗСУВУ:
Регістри зсуву зазвичай є розширенням паралельних регистрів додатковими операціями зсуву. При виконанні таких операцій група зчитаних бітів послідовно зсувається (у прямому або зворотньому напрямку) на додатковий вихід регистру, а звільнені ячейки регістру заповнюються з даних на додатковому вході.
Модель регістра зсуву (.jpg)

Основне застосування регістрів зсуву це перетворення послідовного код в паралельний код або навпаки, а також виконання допоміжних мікрооперацій в арифметичних або логічніх операціях. Наприклад, спощена:
модель послідовного каналу передачі даних (.jpg)

До регістрів зсуву можна також віднести ПЗЗ, тобто прилади із зарядовим зв'язком (англ. CCD, charge-coupled device), в яких застосовується технологія керованого перенесення заряду в об'ємі напівпровідника.

Напрямок зсуву заряду визначається динамікою потенціалів на керуючих електродах Е1,Е2,Е3.
Найбільш яскравим представником приладів цього класу є ПЗЗ-матриця. Але інжекцію заряду можна виконувати не лише фотоелектричним ефектом, тобто джерелом заряду можливо виконувати звичайними електричними підключеннями на канал приладу.

РЕГІСТРИ З ТРЬОМА СТАНАМИ:
Три стани регістру це в першу чергу стани додаткового вихідного каскаду звичайного регістру. Такий вихідний каскад призначений або працювати як звичайний вихід логічного елементу, або блокувати логічний сигнал та переходити у великій вихідний опір, що рівнозначно електричному відключенню логічного елементу від загальної вихідної лінії. Наприклад:
TTL модель троьх станів (.jpg)

РЕГІСТРИ ЗАСУВКИ (Latch):
Цей пристрій містить регістри D-типу та повторювачі виходу з 3 станами. Вхід Latch Enable (LE) призначений для стеження або фіксації вхідних даних вбудованим регістром. Вхід Output Enable (OE) призначений для повтору даних регістра, або відключення пристрою від вихідних ліній (шини даних). Проте, стан відключення не заважає введенню нових даних у регістр.

Приклад побудови регістра засувки наведена в моделі:
логіка регістра D-Latch (.pdf)

Моделі в архіві реалізовані в Multisim версії 11. Кожна супроводжується електричною схемою в форматі pdf.

Заватажити архів моделей (*.7z). Архів включає 6 документованих моделей (.ms11, .pdf)

У рамках WEB-сайту дуже важко докладно представити логіку побудови та реалізацію пристроїв комп'ютерної електроніки. Тому ми зупинимося тільки на ключевих моментах, які в подальшому полегшать знайомство з цим напрямком науки та технології.

Бінарні обчислення:

Бінарні обчислення засобами цифрової електроніки це базова тема для опанування логіки та побудови пристроїв комп'ютерної електроніки. По перше відзначимо, що для створення всього спектру арифметичних операцій достатньо реалізації:

• об'єкта "позитивне число";
• операції зміни знака числа, тобто перетворення позитивного числа на негативне або навпаки (далі таки числа будемо називати числами зі знаком або просто числами);
• об'єкта "модуль числа" - для позитивного числа його модуль це само позитивне число, для отримання модуля негативного числа необхідно змінити його знак на позитивний;
• операції суми чисел.

Зазначимо, що негативне та позитивне число з однаковими модулями є дзеркальним відображення відносно нуля, тобто пустого заначення в вмножині чисел. Також необхідна доступність операцій для побудови алгоритмів, тобто:

• операцій відносин: більше, меньше, дорівнює;
• логічних операцій: not, and, or, xor;
• алгоритмічних операцій: условне та безусловне розголуження.

• операція віднімання двох чисел обчислюється як сума чисел зі знаками;
• операція множення двох чисел (випадок цілих чисел) алгоритмічно виконується додаванням у результат операції модуля першого операнда таку кількість раз, яку має значення модуль другого операнда (якщо знаки операндів однакові - результат позитивний, якщо різні - результат негативний);
• операція поділу двох чисел (випадок цілих чисел) алгоритмічно обчислює яку кількість раз можна із модуля першого опнранда відняти модуль другого операнда доки у модуля першого операнда не залишится залишок меньший за модуль другого операнда (якщо знаки операндів однакові то результат позитивний, якщо знаки різні, то результат негативний).

Ми навели дуже спрощені алгоиритми множення та поділу лише для цілих чисел, але (без додаткової деталізації) зазначимо, що дійсні числа за допомогою масштабних коефіцієнтів можна перетворити в цілі числа, виконати операцию, а потім зробити зворотне масштабне перетворення. Також зазначимо, що на даний час розроблено значна кількість алгоритмів множення та поділу чисел, наприклад: Алгоритми швидкого множення чисел (.pdf)

Звісно, вище наведені лише значно спрощені алгоиритми множення і поділу двох чисел, більш того, лише для цілих чисел. А як же дійсні числа? Без додаткової деталізації зазначимо, що дійсні числа за допомогою масштабних коефіцієнтів можна перетворити в цілі числа, виконати операцию, а потім зробити зворотне масштабне перетворення.

Підіб'ємо деякий підсумок. Якщо ми маємо операції додавання, віднімання, множення та поділу числел, то наступними алгоритмічними кроками буде створення операцій "піднесення в цілий ступінь", "факторіал", а також реалізація широкого переліку функцій, що вже розглядалося в
методах та алгоритмах обчислення елементарних функцій (.pdf)

Визначення об'єкта "позитивне бінарне число" та цого базових операцій

Визначемо об'єкт "позитивне бінарне число" як паралельну комбінацію бітів в позиційній системі з основою два. Позиція біту має назву разряд та відповідний масшкабний коефіціент (2^n, 2^(n-1), ... ,2^1, 2^0). Таке визначення отримало назву "бінарний код/binary code". В реальних комп'ютерних пристроях довжина такого коду обмежена як 8-біт (байт), 2 або 4 або 8-байт (слово/word), 2-слова (подвійне слово/double word). Позначимо окремий біт як "Xi або Yi" де "X або Y" - символ значення біту (1 або 0), а "i" - символ значення разряду (n ... 0). В такому випадку, значення числа (при застосуванні операцій звичайному сенсі) буде мати наступний вигляд:

Xn * 2^n + ... + X1 * 2^1 + X0 * 2^0

Операція суми двох бінарних чисел
Для деталізації алгоритму операції, нам знадобится додатковий біт з назвою "біт перенесення/carry bit" та біт резульнату. Позначимо їх відповідно "Ci" та "Ri", де "i" - символ значення разряду. Операція суми двох бінарних чисел виконується поразрядно для бітів кожного разряду (Xi, Yi, Ci), починаючи з разряду i=0 та значення R0=0. Для обчислення значення біту результата застосовуються логічні операції:

Ri = (Xi xor Yi) xor Ci
C(i+1) = (Xi and Yi) or ((Xi xor Yi) and Ci)

За посиланнім наведемо приклад суматора чисел довжиною напівбайту (.jpg)

Операції зміни знака числа
Основною ідеєю отримання коду негативного числа є пошук такого коду, який будучи підсумований з кодом числа утворює нульове значення. Якщо розглядати суму для чисел з кінцевим числом розрядів, такий код можна отримати шляхом побітової інверсії коду вихідного позитивного числа з подальшим додаванням одиниці та ігноруванням біта переносу.

Наведемо приклад для пошуку негативного бинарного коду для десятичного числа п'ять:

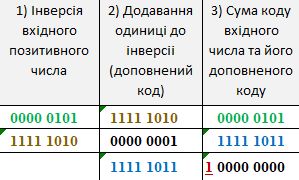
З наведеного прикладу ми бачимо - якщо ігногувати біт переноса (червона підкреслена одиниця), то контрольна сума для пошуку негативного коду буде дорівнювати нулю. Таким чином побітова інверсія вхідного коду с додаванням одиниці, дійсно утворюе негативний код вхідного позитивного числа. Такий код отримав назву "Додатковий/Two’s complement" або в, деяких джерелах, як "Доповнювальний".

В архіві, у папках розділу, наведена модель перетворювача коду у додатковий код (.pdf) , яка дозволяе обчислювати додатковий код для довільних чисел із десятичного діапазону (-1 ... -128).

З наведеного прикладу ми бачимо - якщо ігнорувати біт переноса (червона підкреслена одиниця), то контрольна сума для пошуку негативного коду буде дорівнювати нулю. Таким чином побітова інверсія вхідного коду с додаванням одиниці, дійсно утворюе негативний код вхідного позитивного числа. Такий код отримав назву "Додатковий/Two’s complement" або в, деяких джерелах, як "Доповнювальний".

З основ загальної математики нам відомо, що абсолютне значення позитивного числа та абсолютне значення того же числа со знаком мінус мають одне значення. В комп'ютерній арифметиці абсолютне значення числа со знаком має назву "Модуль числа". Якщо значення модуля позитивного числа дорівнюе значенню самого числа, то дзеркальна (відносно нуля) властивость модуля дозволяе отримувати значення модуля негативних чисел за допомогою поразрядної інверсії додаткового коду з додавання одиниці. Наведемо приклад отримання модуля додаткового бінарного коду десятичного числа п'ять:

На завершення буде корисно неквапливо дослідити бінарні операції плюс та мінус з целими числами за допомогою моделі, що представлена в розділі архіва: Операції плюс та мінус (.pdf)

Для подальшої деталізації теми розділу буде корисним перегянути wiki - посилання на: Стандарт IEEE для чисел з рухомою комою , а також статтю: моделювання та реалізація суматора дійсних чисел (.pdf)

Моделі в архіві реалізовані в Multisim версії 8 та 11, а також як програми на Delphi. Кожна супроводжується електричною схемою в форматі pdf.

Заватажити архів моделей (*.7z). Архів включає 2 документовані моделі (.ms11, .dpr, .pdf)

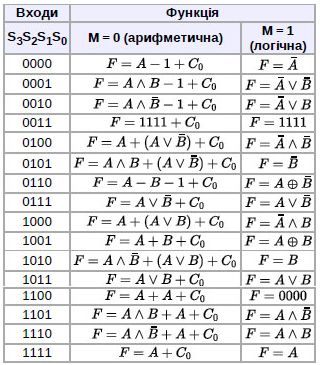
АЛП:

В розділі 4 ми вже перераховували операції, які необхідні для комп'ютерної арифметики цілих чисел, але в наведених моделях показали лище реалізацію операцій плюс, мінус, модуль. В даному розділі наведемо пристрій 74S181N, в якому додано логічні операції та збільшено кількість арифметичних операцій:

Такий пристрій отримав назву арифметико-логічний (АЛП), а його реалізація представлена, як комбінаційна схема АПЛ серії 74 (.pdf) , крім того, в архіві розділу представлена тест-модель арифметико-логічного пристрію (.pdf) , яка дозволяе більш детально ознайомитися з його можливостями.

Центральний процесор:

Сьогодні найбільш повний вигляд, як складу операцій, так і алгоритмів їх реалізації, пропонують пристрої, що отримали назву "Центральний процесор, ЦП (англ. Central processing unit, CPU)". Більшисть операцій в процесорах виконується алгоритмічно (мікропрограмно), та в завершенному вигляді мають назву "інструкції" або "команди". Процесори (с позиції цифрової електроніки) мають дуже складну структуру, тому, як правило, їх опис включає загальну архітектуру, що включає в себе архітектуру команд. На сьогодні, до найбільш відомих архітектур процесорів можна віднести:

• RISC ( Reduced Instruction Set Computer ) архітектура є однією з найпоширеніших архітектур у сучасних процесорах. Її характеризує простота та ефективність виконання базових операцій. RISC процесори мають набір простих інструкцій, що дозволяє їм працювати з великими обсягами даних;
• CISC ( Complex Instruction Set Computer ) архітектура відрізняється великою кількістю складних інструкцій та різноманітністю функцій. Це дозволяє CISC процесорам виконувати складні операції за одну інструкцію;
• SIMD ( Single Instruction, Multiple Data ) архітектура, спрямована на виконання однієї операції над декількома елементами даних одночасно. Це дозволяє розпаралелити обчислення і підвищити продуктивність;
• MIMD ( Multiple Instruction, Multiple Data ) архітектура передбачає виконання різних інструкцій над різними наборами даних одночасно. Це використовується для розпаралеленого виконання завдань;
• Архітектура ARM (Advanced RISC Machine) є однією з найпоширеніших архітектур в сфері мобільних пристроїв та вбудованих систем. ARM процесори відомі своєю енергоефективністю та високою продуктивністю;
• Архітектура x86 є однією з найпоширеніших архітектур для персональних комп’ютерів та серверів. x86 процесори відомі своєю високою продуктивністю.

Всі сучасні процесори мають розвинені можливості обслуговування переривань, роботи з оперативною пам'яттю, шинами адреси та шинами даних. Та окремим рядком треба відначити здатність сучасних процесоров паралельно виконувати інструкції. Така особливость архітектури процесора отримала назву Суперскалярність (Superscalarity). Сенс суперскалярності полягае у завантаженні до вбудованої у процесор пам'яти (кеш-пам'яти) ланцюжків інструкцій (в окремих реалізаціях, мікропограмне складання з таких інструкцій - суперінструкцій), які безумовно будуть виконуватися. Як правило, довжина таких лацюжків визначається і закінчуєтся першим у ланцюжку умовним оператором. Далі такі ланцюжки або суперінструкціі можна паралельно планувати, паралельно виконувати та сінхронізувати між собою апаратними засобами процесора.

Детальний опис архітектури процесорів потребує, як мінімум, книги з великою кількістю сторінок, а то і декілька таких книг. Наприклад, тільки скорочена довідка по архитектурі x86 має вже помітно значний обсяг. Тому, для досягнення професійного рівня усвідомлення матеріалу використовуйте літературу, надану в wiki-посиланнях. В україномовній Вікіпедії корисни буде посилання:
сторінки в категорії «Процесори»

Зрозуміло, що окремо від обчислювальної системи процесор є не більше, чим просто електронна мікросхема або пристрій. Тому на завершення розділу наведемо, як приклади окремих мікропроцесорів, так и відносно простих обчислювальних систем, таких як персональні комп'ютери (ПК): Архітектура ПК (.pdf) Інформацію по більш складним обчислювальним системам (наприклад Блейд-серверам, Мейнфрейм або Суперкомп'ютерам), сьогоді можна легко знайти в інтернеті (наприклад за допомогою Google).

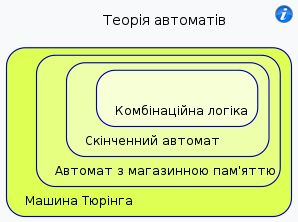
СКІНЧЕННІ АВТОМАТИ:

Теорія автоматів так ж нескінченна тема як і теорія ком'ютерних систем. На підтвердження цієї тези наведемо посилання на загальні категорії теорії автоматів , а також категорії теорії скінчениних автоматів .

В рамках цьго розділу ми зосередим увагу на лише скінченних автоматах, що призначені для керування об'єктами з кінцевою кількістю станів. Такі автомати допомагають розв'язувати багато задач, серед яких автоматизація проєктування електронних приладів, проєктування комунікаційних протоколів, синтаксичний аналіз та інші інженерні застосування.

Скінченний автомат (англ. finite-state machine), автомат зі скінченною множиною станів це:

1. математична або евристична модель, у якій визначаеться послідовність зміни станів об'єкта в залежності від його поточного стану та доступної інформації у цьому стані, а також для кожного поточного стану визначається необхідні керуючі дії, спрямовані на об'єкт;
2. реалізація цієї моделі апаратними або програмними засобами.

Проектування скінченного автомату починається з визначення кількості і сенсу його станів. Як правило, окремим станом об'єкта вважається ситуація, коли керуючому автомату для успішного керування об'єктом нема необхідності відстежувати інший перелік вхідної інформації та змінювати склад керуючих дій. Саме тому, типовий опис автомата, як мінімум, включає три таблиці:

• Таблиця вхідної інформації. Далі просто таблиця вхідних сигналів або "Таблиця входів";
• Таблиця переходів між станами автомату або просто "Таблиця переходів" Переходи між станами автомату повинна виконувати функція переходу, яка аналізуе поточний стан автомата, поточні вхідні сигнали та визначає новий стан для автомата;
• Таблиця керуючих дій. Далі просто таблиця вихідних сигналів або "Таблиця виходів".

До класичних скінченних автоматов традиційно відносять два типи автоматів:

1. Автомат Мура (.pdf) або Moore machine
   Блок-функціональна струнура такого автомата має наступний вигляд;
   
   
   
   Автомати Мура, в електрониці, реалізуються на базі комбінаційних схем та тригерів (типово асинхронних RS-тригерів).


2. Автомат Мілі (.pdf) або Mealy machine
   Автомат Мілі відрізняється від автомату Мура лише тим, що у формуванні вихідних сигналів використовується не лише поточний стан, а ще і вхідні сигнали.

В якості приклада реалізації скінченного автомату, наведемо автомат для керування аналоговою частиною АЦП двократного інтегрування(.pdf) , та його лічильника інтервалів інтегрування.

Представлена логіка роботи АЦП, дозволяє виділити чотири стани в роботі АЦП, тобто, начальний стан, стан інтегрування вимірюваної напруги, стан інтегрування напруги опорного джерела, а також стан зупинки для фіксації результату.

Подальше проектування будемо виконувати відповідно до послідовності, що пропонує методика проектування таблиць автомату(.pdf)

Як резултат проектування, ми отримаємо:

1. реалізацію автомата (.jpg) для керування АЦП;


2. діючу Multisim модель АЦП двократного интегрування:
   модель АЦП(.pdf) .

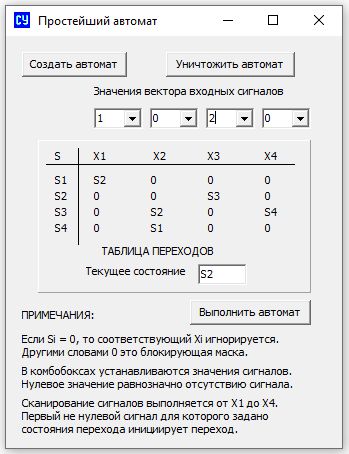
У методиці проектування таблиць автомату, пунктами 8 ... 10 було показано, що ідеологію скінчених автоматів можна застосовувати у комп'ютерних програмах. На малюнку представлена діалогова форма програми, де засобами ООП Delphi розроблено автомат з програмно завантаженими таблицями.

На завершення розділу зазначимо, що програмно реалалізовані автомати із вбудованою або додатковою стековою пам'яттю - це важливі елементи а архітектурі компіляторів, планувальників та диспетчерів виконання програм, модулів та об'єктів.